Lesson 12: NailingPlanks (Nailing Planks)

Lesson 12:  NailingPlanks
https://codility.com/programmers/lessons/12

This is a tough question, so let's do this step-by-step.
First the simplest solution, then the O((N+M)*log(M)) solution, and the O(M+N) solution.

(1) The simplest solution

The problem suggests the O((N+M)*log(M)) time complexity for this problem, and log(M) suggests the binary search is done for M (for the number of nails).

The simplest strategy is to perform the binary search for the required number of nails, and check if all the planks are nailed.

The below is the simple implementation for this strategy, however while it gets the 100% score for the correctness, it gives the 0% performance score; this is a matter of course. This is not a O((N+M)*log(M)) solution. 

(I guess the time complexity of this code is like O(N * M * log(M)) or so...)

#include <alloca.h>
#include <memory.h>

int check(int k, int* nailed, int* A, int* B, int N, int* C, int M)
{

    int i;
    for (i = 0; i < k; i++){
        int j;
        for (j = 0; j < N; j++){
            if (A[j] <= C[i] && C[i] <= B[j]){
                nailed[j] = 1;
            }
        }
    }
 
    for (i = 0; i < N; i++){  
        if (nailed[i] == 0){
            return 0;
        }
    }
 
    return 1;
}

int solution(int A[], int B[], int N, int C[], int M)
{
    int nailed_size = sizeof(int) * N;
    int* nailed = (int*)alloca(nailed_size);
 
    int beg = 1;
    int end = M;
 
    int min = M + 1;
    while(beg <= end){
        int mid = (beg + end) / 2;
        memset(nailed, 0x00, nailed_size);
        if (check(mid, nailed, A, B, N, C, M)){
            end = mid - 1;
            min = mid;
        }
        else {
            beg = mid + 1;
        }
    }
 
    return min == M + 1 ? -1 : min;
}


(2) The O((M+N) * log(M)) solution

So now we know the problem in the previous solution is the time complexity of the 'check' function, and need some more improvement if the given nails can nail all the planks.

We use the 'prefix_sum' algorithm that we learned in the Lesson 3. 
First, we clear the array, prefix_sum[] with 0, and then add 1 to prefix_sum[i] if there is any new nail found at the position 'i'.

Then we compute the prefix_sum for the total number of nails found so far until the position from head to tail.

When we check if there is any nail that can nail each plank, we only have to use this prefix_sum; if there is no nail between A[i] and B[i] (within the plank 'i'), prefix_sum[B[i]] == prefix_sum[A[i] - 1].

The part to compute the prefix_sum array is O(M) and the part to check planks is O(N). So when combined, the whole time complexity for these two parts is O(M+N).

As we repeat this by binary search, the whole time complexity of the code is O((M + N) * log(M)), as this problem requires.

This strategy gives the 100% score.

#include <alloca.h>
#include <memory.h>

int solution(int A[], int B[], int N, int C[], int M)
{
    int prefix_sum_size = sizeof(int) * (2 * M + 1);
    int* prefix_sum = (int*)alloca(prefix_sum_size);
 
    int beg = 1;
    int end = M;
 
    int answer = -1;
    while (beg <= end){
     
        int mid = (beg + end) / 2;
        memset(prefix_sum, 0x00, prefix_sum_size);
     
        int i = 0;
        for (i = 0; i < mid; i++){
            prefix_sum[C[i]]++;
        }
     
        for (i = 1; i <= 2 * M; i++){
            prefix_sum[i] += prefix_sum[i - 1];
        }
     
        int failed = 0;
        for (i = 0; i < N; i++){
            if (prefix_sum[B[i]] == prefix_sum[A[i] - 1]){
                failed = 1;
            }
        }
     
        if (failed){
            beg = mid + 1;
        }
        else {
            end = mid - 1;
            answer = mid;
        }
    }
 
    return answer;
}

(3) The O(M+N) solution

I usually google solutions by other people so to see if there is any better solution. 

And found one interesting approach by a Chinese guy here.
http://blog.csdn.net/caopengcs/article/details/41834173

As his explanation is entirely written in Chinese, I don't get any meaning, so I read his source code in the above link.

Here is the solution I re-coded so to make it more readable. I also added lots of the comments. However, the code may not be enough to grasp what is done quickly, I add some explanation after the code.

As we want to shorten the code without complicating it by using some data structure (double-ended queue), we used C++ (not C as so far) this time so to simplify the code.

This code gives the 100% score. 

#include <deque>

using namespace std;


int solution(vector<int> &A, vector<int> &B, vector<int> &C)
{
    int max_pos = C.size() * 2;
   
    //this vector holds -1 at nail_at[i] if there is no nail at the position i
    //and k (the number of the nail) if there is.
    vector<int> nail_at;
    nail_at.resize(max_pos + 1, -1);
   
    //as two or more nails can be at the same position,
    //we scan C from tail to head so that we can retain the nail with 
    //the smallest index at each position.
    for (int i = (int)C.size() - 1; i >= 0; --i){
        nail_at[C[i]] = i;
    }
   
    //this vector holds -1 at plank_end_at[i]
    //if there is no plank ends at the position i,
    //and the beginning position of each plank, if there is.
    vector<int> plank_end_at;
    plank_end_at.resize(max_pos + 1, -1);
    
    for (unsigned int i = 0; i < B.size(); i++){
        //if there is any two or more planks that end at the same position,
        //we only have to consider the smallest one.
        plank_end_at[B[i]] = max(plank_end_at[B[i]], A[i]);
    }
   
    //a fifo queue to store the nail information.
    deque<int> nail_pos_deque;
   
    //we have checked all the nails until this position
    //if it should be used or not.
    int checked_until_here  = 0;
    int nail_scan_pos       = 0;

    //the minimum number of nails  
    int min_nails = -1;
   
    for (int i = 1; i <= max_pos; i++){
        //there is no plank end at there, just continue scanning.
        if (plank_end_at[i] == -1){
            continue;
        }

        //there is a plank, but its begining position has been already checked.
        //This means that there is al least one plank successfully nailed and
        //this plank can be also nailed together when the plank(s) was nailed.
        //so we can simply neglect this plank.
        if (plank_end_at[i] <= checked_until_here){
            continue;
        }
       
       
        //now we need to check if there is any nail that can nail this plank.
        //first, we have to discard all those nails in the queue that don't
        //nail this plank.
        checked_until_here = plank_end_at[i];
        while ((!nail_pos_deque.empty()) &&
                nail_pos_deque.front() < checked_until_here){
            nail_pos_deque.pop_front();
        }
               
        //nail_scan_pos is the place we scan nails.
        //if we found one at nail_at[nail_scan_pos], we put the information
        //into the deque. So all those nails that appear before nail_scan_pos
        //is currently in the queue or already discarded from it.
        nail_scan_pos = max(nail_scan_pos, checked_until_here);
       
        //now 'i' is the end of the plank curretly under examinened.
        //so we scan any new nail until this position.
        for (   ; nail_scan_pos <= i; nail_scan_pos++){
           
            //no nail found at the current position, just go ahread.
            if (nail_at[nail_scan_pos] == - 1){
                continue;  
            }
           
            //found a nail at the current position.
           
            //now, we can discard away any nails that we don't use anymore.
            //those nails on the left and with a larger index in C[] will never
            //be required again.
            while((!nail_pos_deque.empty()) &&
                   nail_at[nail_pos_deque.back()] > nail_at[nail_scan_pos]){
                nail_pos_deque.pop_back();
            }
            nail_pos_deque.push_back(nail_scan_pos);
        }
       
        //if the queue is empty, there is no nail for this plank.
        if (nail_pos_deque.empty()){
            return -1;
        }
       
        min_nails = max(min_nails, nail_at[nail_pos_deque.front()]);
    }
   
    return min_nails + 1;
}


Now, let's describe what this code really does.

First, we prepare the nail_at array. Each cell of this array, nail_at[i], is associated to the position 'i' and the value at the cell will be -1, if there is no nail at the position 'i', or the index of the nail in the array C, if there is any nail. 

The reason why we can the array C from tail to head, is that there can be two or more nails at the same position. Clearly, since we want the smaller number of nails to use in this problem, we only need the nail with the smallest index among them and can neglect other nails at the same position.


Then we prepare plank_end_at array. Each cell of this array, plank_end_at[i], is associated to the position 'i' similarly. The value of the cell is -1, if there is no plank that ends at the position, or the beginning position of the plank if there is any plank that ends at the position.

What if there are two or more planks that ends at the same position?
We only have to leave the shorter plank among them (or the plank with the largest beginning position ('A[i]') among them). 

To understand why this is fair, see the figure below. Clearly, any nail that can nail the plank A can nail plank B too. Let's suppose i < j. Then, the final answer for this problem is not affected by the i-th nail, as the j-th nail must be used anyway for the plank B. On the other hand, if j < i, we prefer to use the j-th nail for both planks, since using the j-th nail clearly contribute to obtain the minimum number of nails. So even if we neglect plank B, there is no problem in both cases; this is why we would like to pick up the smallest plank among all the planks that share the same end position.

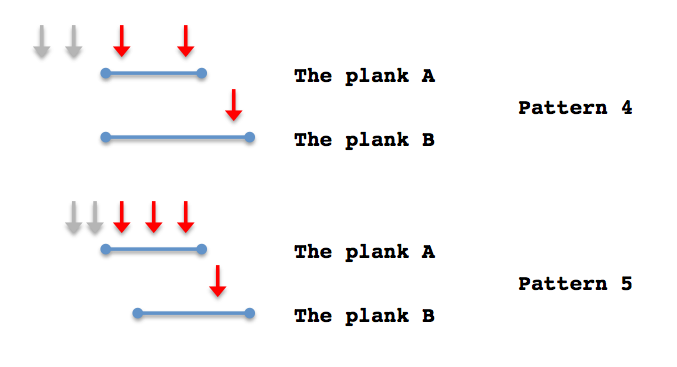
Now, we describe the core part of this algorithm. First, since we scan the plank_end_at[] array from head to tail, it can be said that we check planks sorted in the ascending by their end positions (though we didn't actually sort anything. However, it would be fair to consider the part to prepare the plank_end_at[] array as a bucket sort). As we omit some planks that share the end position with others, there are only five patterns when we arbitrarily pick up two planks. As in the below figure.

Pattern (1): the plank B starts at exactly where the plank A ends o

Pattern (2): the plank B starts after the end of the plank A with some gap.

Pattern (3): the plank B starts before the beginning position of the plank A. 

Pattern (4): the plank B starts exactly at the beginning position of the plank A. 

Pattern (5): the plank B starts after the beginning position of the plank A with some gap.


In any of the patterns above, after checking the first plank, we want to keep any nails that may nail down the next plank. At the same time, after we checked the first plank, we can forget any planks that do not contribute to check other planks.

For instance, in the pattern (1) and pattern (2), after checking the plank A, we can forget any nail whose position is before the beginning point of the plank B. As shown in the below figure. Those nails of grey in the figure can never nail the plank B. We simply can forget about it after we check these.

How about other patterns? In pattern (3), any nail that nail the plank A will plank B. So even if we forget any nail before the beginning of the plank B, as long as there is any nail that nail plank A nails the plank B, as shown in the below figure.

As already mentioned, what we need is the minimum number of nails that can nail all the plank. So even if there is any nail with the smaller index between the beginning of the plank B and the beginning and of the plank A, or the end of the plank A and the end of the plank B (those grey nails in the below figure), these nails won't contribute to contribute to the final answer; suppose any of grey nails are with the smaller index than the red nail. The plank A must use the red nail anyway, so using the red nail instead of grey nails doesn't change the final answer to this problem.

This also means we can throw away any nails before the beginning positions of the plank A, as they won't contribute to the answer. As long as we still remember the nails that appears exactly at and after the beginning position of the plank A, there is no problem; even if we forget any nails that appears before the beginning position of the plank A, even when checking the plank A, there won't be any problem.

In the pattern 4 and the pattern 5, as the beginning position of the plank B is exactly at or after the beginning position of the plank A, even if the nails before the beginning position of the plank A are forgotten after checking plank A, it is clear that there is no problem, as described in the below figure. It should be noted that as shown in the patter 5 of this figure, what is required is not to forget those nails exactly at or after the beginning position of the plank A, as it may nail the plank B. 



From the above discussion, if we check the planks sorted in the ascending order by their end positions, it is clear that we can forget any nail that appears before the beginning position of the plank that we are currently checking.

We want to remember only those nails that might contribute to the final answer, and for this purpose, we only have to remember that nails that appears after the beginning position of the plank that is currently checking. Forgetting the nails that appears before this position do not contribute to the answer.


To remember the nails appear until the current scanning position, we can use the double-ended queue. (The reason why it is not simply a FIFO queue is discussed from the next paragraph). 





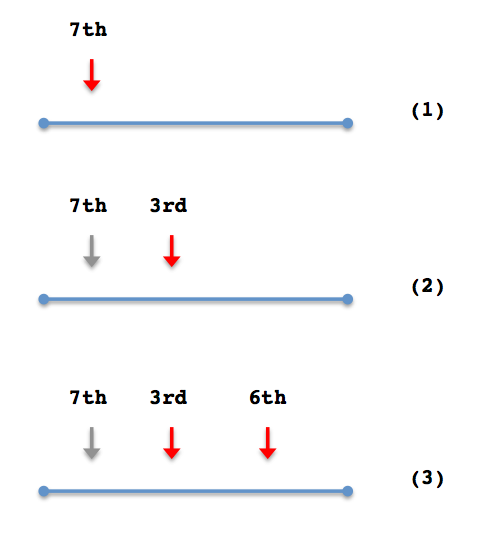
Now, let's discuss which nails we should remember while scanning a plank. We scan the plank from the left to the right as in the below figure. Then, we found a nail that can nail this plank (see (1) of the below figure). 

Let's say first we found the 7th nail. So we put this nail into the queue.  Remember just remembering the position is okay, as the nail_at[] array can be used as a dictionally to get the index of the nail in the array C[] by using the position of the nail. This nail may contribute to nail the next plank.

Then, we keep on scanning to the right, and we found another nail that nails this plank, and it was 3rd nail (see (2) in the above figure). Clearly, we want to use this nail for this plank, as what we want to obtain is the minimum number of nails to be used, which can be picked up from the array C[], from its head to tail.

So we can forget 7th now. Why? As we are investigating planks in the ascending order sorted by the end positions of the planks, any plank that can be nailed down by 7th can be also nailed down by 3rd (since the 3rd nail is located to more right than the 7th nail). These  planks also prefer the 3rd nail. So the 7th nail is now useless. 

We keep on scanning to the right again. We found the 6th nail. Should we keep this nail? Yes, because those planks we scan later that can not be nailed by the 3rd nail may be nailed by this 6th nail. 

What should we do for the 3rd nail now? We would like to remember it , since if the next plank can be nailed by both the 3rd and 6th, we would like to use the 3rd as 3 < 7.

What should we do if we found the 5th nail after the 6th nail? Yes, we should discard the 6th nails from the queue and instead put the 5th nail, as the 5th nail is located more right than the 6th, which means 5th nails can nail any plank, which we may check in the future, if it can be nailed by the 6th plank. Also we would like to use the nail with the smaller index. 

To summarize this, we want to keep the queue with the condition as follows.

(1) the position of the nails put in the queue must be sorted in the ascending order by the positions of the nails. 

This is important, since we want to forget those nails that appears before the beginning of the next plank. We only have to check the head of the queue and discard it if the position of the nail is smaller than the beginning position of the next plank. 

(2) The index of the nails in the queue should be also in the ascending order.

First, this makes it easy to pick up the nail to be used for this plank. If the first nail in the queue after scanning between the begging and ending position of the plank has the smallest index in the array C[], we only have to check the head of the queue and use the position to look up the nail_at[] array to obtain the index of the nail at the position.


To do this, using the double-ended queue is better, because when we discard the nails before the beginning position of the current plank, we discard from the head of the queue, but when we are checking each plank, we discard from the back. Double-ended queue is clearly appropriate for such manipulations.




The above solution implements such a strategy.

(1) We scan plank_end_at from 0 to M * 2. If there is no plank that ends at the position, we progress to the right. 

(2) If we find a new plank that ends at the position, but its beginning position is located more left than or the same as the position we have checked so far (== the max beginning position of the planks that we have checked so far), we can skip this plank; the planks we have so far is already nailed and the nail used for the plank can also nail this plank. 

See Pattern 3, 4. The nail used for prank A are all included within the plank B.

(3) If the beginning position of the next plank is larger than the position we have checked so far (== the max beginning position of the planks that we have checked so far), then we have to check this plank. (See Pattern 1, 2, 5).

However, as we know that any nails that appears before the beginning of this plank won't contribute to nail this plank and other planks we check in the future, we can discard them from the dequeue.

We also would like to update the position we have checked so far, since the current plank's beginning position is located right from the old position.

(4) Then, we begin scanning if there is any new nail to nail this plank, while there are some still remain in the queue.

For example, in Pattern 1, there is a nail that located at the end position of the plank A, and the plank B also starts from the same position. This nail still lives in the queue). For another example, in Pattern 5, the first nail in the plank A is already discarded since it is located left to the beginning position of the plank B, yet other two nails are still in the queue.

When we found a new nail while we are proceeding, we check the last nail in the queue (from the back of the queue) and compare it to the new nail, if its index is larger than that of the new nail. If so, the old nail in the queue will be discarded. We do this until we found no more nail in the queue meet this condition.


(5) Now we finished scanning and reached the end position of the current plank. If there is no nail that can nail this plank, the queue is empty. So the answer will be -1 (we can't nail all the planks even when using all the nails).

(6) If the queue is not empty, the first nail in the head of the queue has the smallest index number among all the nails that can be used to nail this plank. we pick this up and update the min number of the nails, if it is bigger than the current one.

(7) After scanning from head to tail of panks_end_at[], we add one to min_nails, as we used the index no. (remember that the array is zero indexed and the min_nails contains the index of the array C[].)


This is what we do in the above solution.








Now, let's see the time complexity of the above algorithm.


The time complexity the first loop to make the nail_at array depends on M and that of the second loop to make the plank_end_at array depends on N. 

As for the last nested loops, the outer loop depends on M. The inner while-loops to pop the dequeue won't repeat more than M times (as this dequeue just added the nails, at most just one time for each nail and some nails won't be added). The repetition of the while loops are not dependent on the outer loop. 

Similarly, the inner for-loop just repeat M times, independently from the outer loop. The outer loop only defines the upper limit of the loop, and nail_scan_pos just keep on increasing from 0 to max_pos, and never decreases.

So as for this part, the whole time complexity just depends on M.

Combining these three parts gives the time complexity of O(M+N).